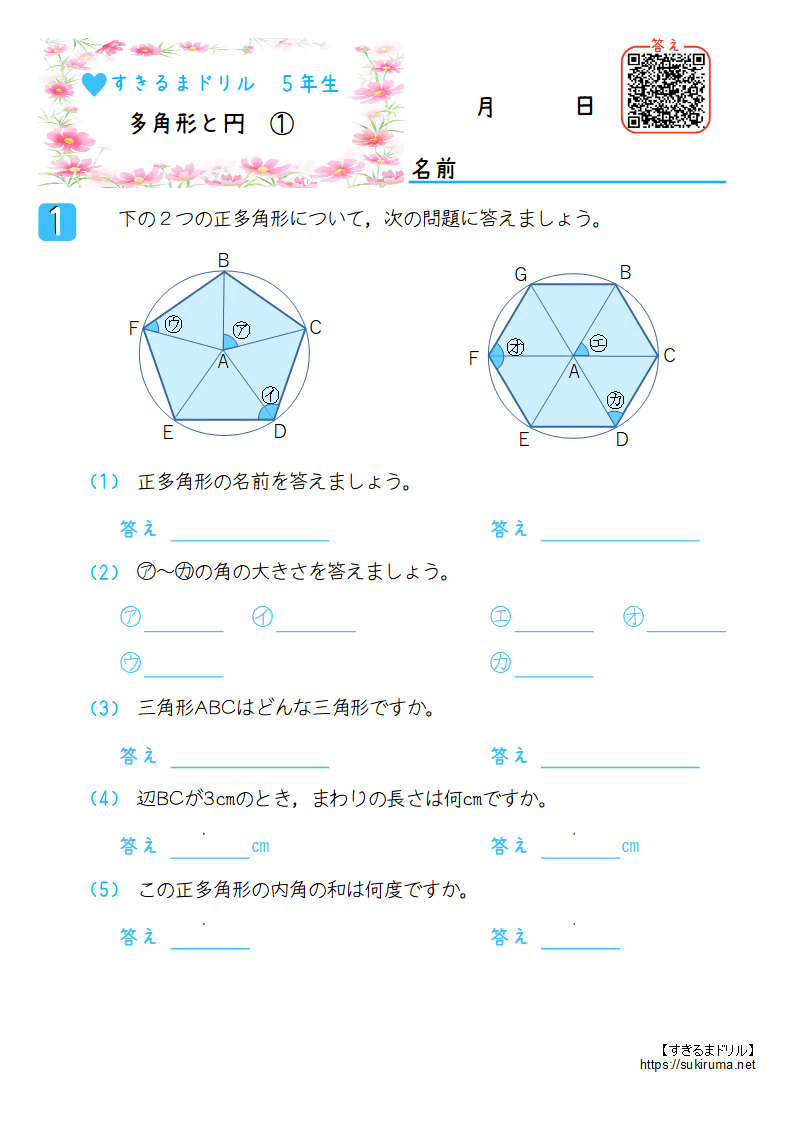
多角形と円 ① 名前 下の2つの正多角形について,次の問題に答えましょう。 正多角形の名前を答えましょう。 答え 正五角形 答え 正六角形 ㋐~㋕の角の大きさを答えましょう。 ㋐ 72° ㋑ 108° ㋓ 60° ㋔ 1° ㋒ 54° ㋕ 60° 答え 二等辺三角形 答え 正三角形 答え 15 ㎝ 答え 18 ㎝ この正多角形の正多角形と円/理解シート 正五角形・正六角形の辺の長さや角の大きさは,どうなっているの 無断複製・転載・翻訳を禁ず GAKKEN B Title 算数 Author①円周率の正六角形の面積での近似 円周の長さで比較するより、「円の面積は内接正六角形の面積より大きく、外接正六角形の 面積より小さい」という比較の方が大小関係は明瞭でわかりやすいし、多角形の面積を求める 教材にもなる。よって、面積の
Kids Gakken Co Jp Box Sansu 05 Pdf B Pdf
円と正多角形 直径の求め方
円と正多角形 直径の求め方-正多角形の外接円 Very goo tools! 多角形の面積で円周率を求める はじめに 半径 \(r\) の円の面積は \(\pi r^2\) ですから、半径1の円の面積は \(\pi\) です。 従って、半径1の円に内接する4角形, 8角形, 16角形 の面積は円周率 \(\pi\) に近づいてゆくはずです。



1
水力直径(すいりきちょっけい、英語 Hydraulic diameter )とは、非円形の管および水路で流れを扱う際、円管の直径に相当する長さを表す量である。 = ここで、 D H が水力直径、 A は流れの断面積、 P は断面のうち濡れている部分(濡れ縁)の周長である。 また、4倍せず単純に流れの断面積を方法2正多角形で円を挟んで円周率を絞り込む 円を正多角形で挟みます。 たとえばわかりやすい例として、正方形で円を挟むと考えましょう。円周は 内接する正方形 よりは大きいけど 外接する正方形 よりは小さいというのが分かると思います。 直径 × 円周率 = 2 × 半径 × 円周率 = 円周の長さ 円の半径を r としたら、その2倍が直径 2r 。 ですから、円の直径(2r)に円周率(π≒314)をかけることで円周の長さ(2πr ≒ 628r)が求まります。 例題①:半径5cmの円の、円周の長さを求めて下さい。
多角形41/コンパスと直線定規を使った正八角形の描き方 円に内接する「正八角形」の作図 コンパスを使って描いた円を基準にして正八角形をを描く方法です。 ☆用具:直線定規、コンパス (1) 基準となる直線上の点oを中心に円を描き、円と直線の交点abを求める。 (2) コンパスを使い、点a「円の面積の求め方」を とらえられるようにしています。 動画作成協力・・動くイラストフリー素材 この動画の説明は以下の文章でご覧下さい 「円周率と円周と直径・半径」の勉強を忘れている時は、5年の「円と正多角形」でおさらいをしまょう。21 円に内接・外接する正多角形 N を自然数とする.半径1の円に内接する正N 角形の一辺の長さを2a,外接す る正N 角形の一辺の長さを2bとする.同様に,半径1の円に内接する正2N 角形 の一辺の長さを2a′,外接する正2N 角形の一辺の長さを2b′ とする.これ
正多角形の角数をどんどん増やしていけば、求められる円周率の精度が上がりますね。 正多角形による円周率の近似 直径 \(1\) の円に外接、内接する正 \(6 \cdot 2^n\) 角形の周の長さをそれぞれ \(a_n\) , \(b_n\) とおくと、正多面体 (せいためんたい) とは、すべての面が合同な正多角形で、かつすべての 頂点 (ちょうてん) に同数の面が集まっている多面体です。 凸 (とつ) 正多面体には5 種類 (しゅるい) ありますが、ここでは正四面体と正八面体の体積の公式を 挙 (あ) げます。多角形と円 ③ 名前 式 × = 答え 157 ㎝ 次の円周の長さを求めましょう。 答え 14㎝ 答え 26㎝ 答え 471 ㎝ 答え 3768㎝ 答え 49㎝ 答え 2355㎝ 次の円周の長さを求めましょう。 答え 2512㎝ 答え 7536㎝ 答え 3454㎝ すきるまドリル 5年生 直径5㎝の円があり



正多角形の内接円の半径 倭算数理研究所



Kids Gakken Co Jp Box Sansu 05 Pdf B Pdf
正多角形の描き方 正三角形や正方形は三角定規を使って簡単に描くことが出来ます。正六角形の描き方も多くの方が知っていると思います。 コンパスを使って円を描き、そのままの半径で円周をプロットし、円との交点を結べば正六角形が完成します。 一辺4センチの正六角形を描くならば正多角形と円/理解シート 円周から,直径・半径を求める方法を教えて 無断複製・転載・翻訳を禁ず GAKKEN B Title 算数 Author VAIO Created Date 926 PM①正多角形の意味 ②正多角形のかき方 ③円周率の求め方(円の円周と直径の関係) ④円周や直径の求め方 ⑤生活の中で円周を求めるよさ 教え方1 正六角形や正八角形を作らせながら、正六角形や正八角形の意味をとらえさせます。




円周の求め方 円周率とは何か なぜ無限に続くのかを説明 その割り切れない理由について アタリマエ
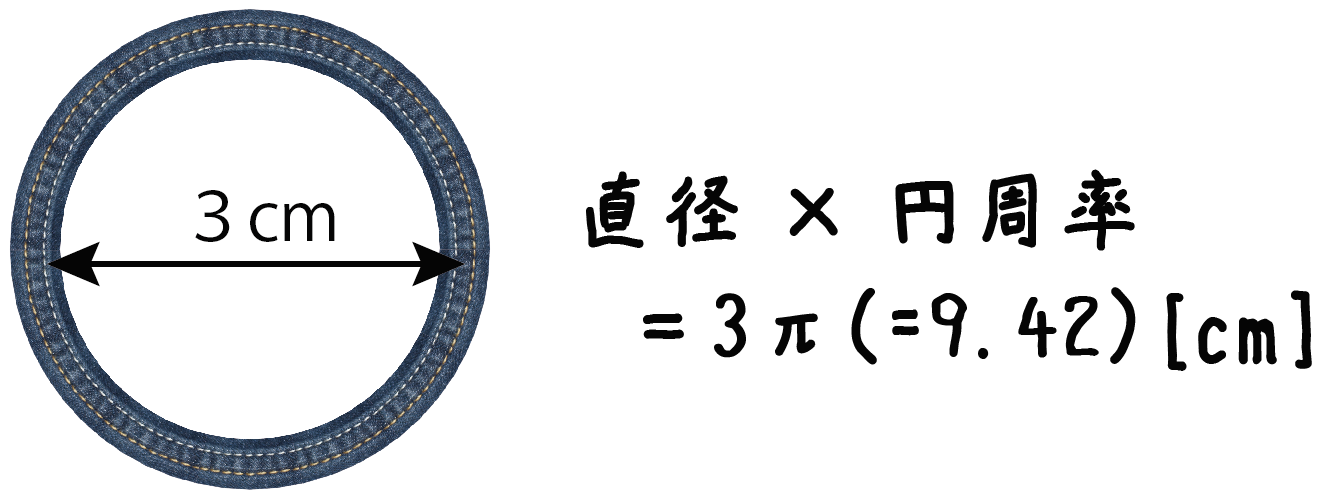



直径から計算 円周の長さの求め方 の公式を3秒で覚える方法 Qikeru 学びを楽しくわかりやすく
5年 学研教育情報資料センター 算数 学習相談 小/算数/5年/図形/ 正多角形と円/理解シート まずは、円に内接する正多角形の面積について説明します。まずは、考え方のポイントからです。 正\(n\) 角形の面積 \(=\) 三角形の面積 \(\times n\) このポイントを踏まえて、早速例題です。 例題 半径\(2\) の円に内接する正八角形の面積を求めよ。 解くときに大事なことは、上のポイントΦ600の内接する正八角形の1辺の長さを求めたかった ご意見・ご感想 円の半径r=300でのn=8の多角形の1辺の長さaはではなくて?ではないでしょうか。 keisanより r=300の時、辺の長さがとなるのは、 円に外接する正多角形と考えられます。




この2つのやり方教えてください お願いします Clear




算数 5年生 正多角形と円 円周率 授業力アップ 学級経営の話
5年算数 円と正多角形 2 子どもの学習支援 by いっちに算数 スマホ版 前のページにもどる ↑正多角形の書き方(アニメ) 教え方3 教え方3-① 円周と直径の意味を教え、円周の長さと直径の長さの関係を調べさせ、円周率を理解させます。 直径は、半径の2倍の長さです 円の周(まわ)りを円周三角形の面積を使って内接円の半径を求める 内接円の半径を r とおきます。 内接円の半径を求める公式 より、 r = 2 S a b c です。 また、 正三角形の面積の求め方 より、 S = 3 4 a 2 が成立します。 よって、 r = 2 × 3 4 a 2 a a a = 3 6 a類似点に気づく 多角形の面積の求め方も、辺心距離(a) x 外周(p) / 2というものでした。外周は1辺の長さ(s)に辺の数(n)を掛けることで求められます。通常の多角形の場合、nは全体を構成する三角形の合計の数も意味します。 つまり、この公式は1つの三角形の



Http Www Boe Kashiwa Ed Jp Action Common Download Main Upload Id 6032



正多角形の描き方
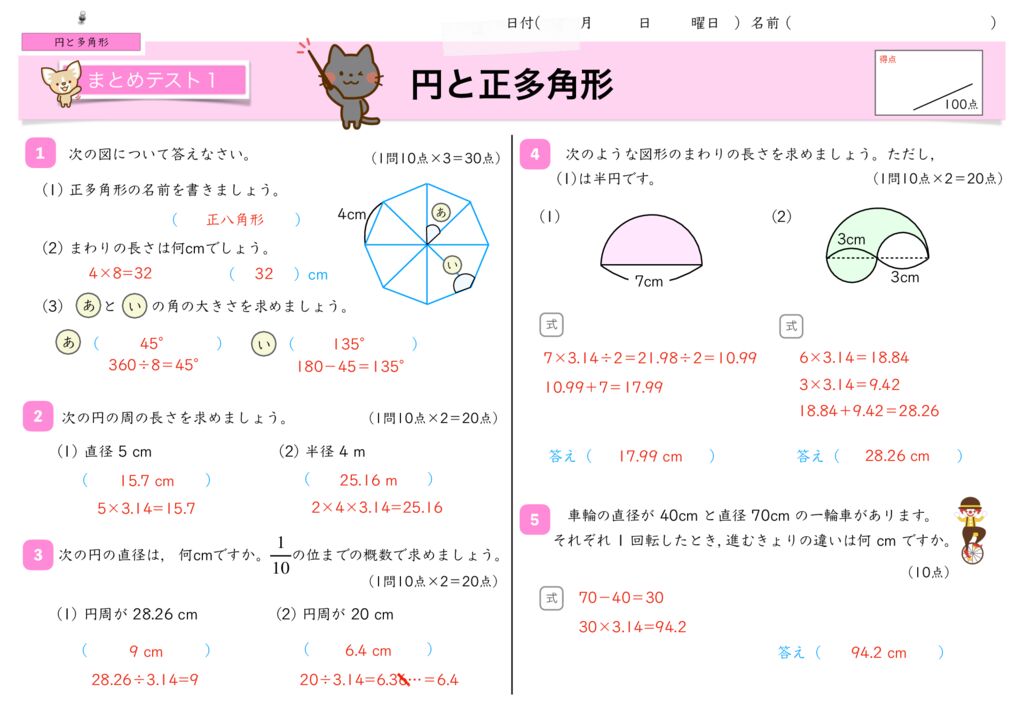
5年 学研教育情報資料センター 算数 学習相談 小/算数/5年/図形/ 正多角形と円/理解シート正多角形と円 4① ₁ ある車いすのタイヤの円周の長さは176cm ありました。 このタイヤの直径の長さを求めましょう。 ① 直径の長さを cm として,( )にあてはまる数を 書きましょう。 (10 点) ② このタイヤの直径は約何cm ですか。四 し 捨 しゃ 五 ご 入 にゅう して, 1 10 の位までの円周の求め方: (円周の長さ) = (直径) × (円周率)




円周の公式 なぜ直径 円周率で計算できるのか 円周率を調べる方法 数学fun




5年生算数 正多角形と円 円周の長さと直径の長さの関係を調べよう Youtube
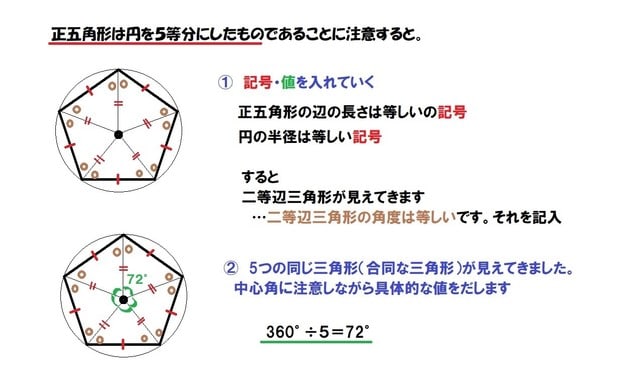
円に外接する正多角形 底面から柱へのステーの長さを算出させていただきました。 使い易いです。 ありがとうございました。 aの計算式ってあってますでしょうか? 計算自体はあってるのですが、式が違う気がするのですが 関数電卓で計算すると 私としては、円周の半分と直径を対比して、円周の半分 ÷ 直径 = 158倍・・・ とした方が分かりやすいと思うのですが、それはともかく、結局、この式から分かったのは、真円の半径の正体とは、真円に内接する正多角形(0°~90°)の1辺1辺に対するsinの値の総和であるということでした。等しい多角形を正多角形といいます。 13 正答例と解説 5年「正多角形と円周の長さ」 〔考え方のポイント〕 正六角形の性質を使って円周の長さを求めよう 答え( イ・エ ) 円の中心のまわりを,グループの数で等分した正多角形を考 えます。 グループの数は,学級の人数である30の約数で




正多角形をプログラムを使ってかこう 杉並区立西田小学校 未来の学びコンソーシアム



内接多角形と外接多角形から円周率を求める
正九角形の1つ分の内角は\(=140°\) 正十角形の1つ分の内角は\(=144°\) 正十二角形の1つ分の内角は\(=150°\) と求めてやることができます。 内角の和を考える方法 次は内角の和から1つ分の大きさを求める方法です。 まず、多角形の内角の和は技・円を使って正多角形をかくことができる。 ・円周率を用いて直径から円周の長さ,円周から直径の長さを求めることができる。 知・正多角形の意味や性質を理解する。 ・円周率の意味や直径,円周,円周率の関係及びその用い方を理解する。 関連※比較・検討場面で「考え方の関連付け5年 学研教育情報資料センター 算数 学習相談 小/算数/5年/図形/ 正多角形と円/理解シート



1



Www Shinko Keirin Co Jp Keirinkan Sho Sansu Support Keyseat Data Sansu 5nen3 02 Pdf
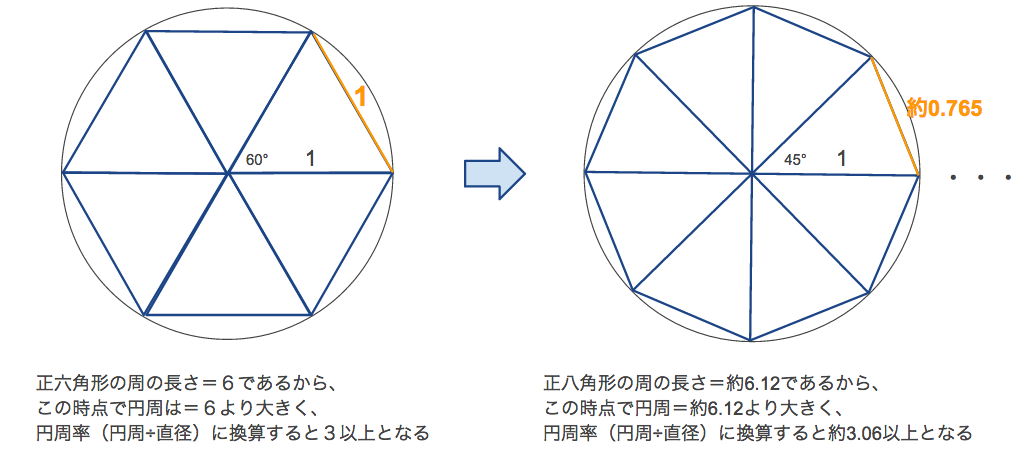
このようにして円周長の近似値を求め、直径で割ることで、円周率を求めるのである。 正多角形の角の数が無限に多ければ、それは円そのものになる。 次のページでは、多角形を用い円周率の近似値の求め方を解説する。 次のページ:多角形による円周率④面積の求め方のくふう p144 1 p146 1 ⑤面積と比例 p147 1 ⑩平均とその利用 ①平均 p151 1 p152 3 p153 5 p154 8 ②平均を使って p155 1 ⑪単位量あたりの大きさ p159~160 1 p161 3 p162 1 ⑫分数 (2) ①わり算と分数 p165 1 p165 2 p166~167 1 ②分数と小数・整数の関係 p168 1 p168 3 p169 5 ⑬割合 ①割合先の投稿にもありましたが、直径も表示されると更に良いと思います。 直径も表示されるようにしました。 直線を曲げたときの弧の長さの差が規定値以下になる半径rを求めていました。 すごい。 感激 便利で助かります
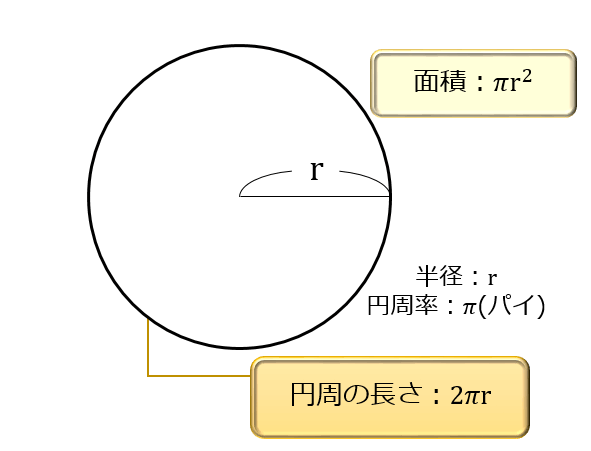



円周の求め方 円周率とは何か なぜ無限に続くのかを説明 その割り切れない理由について アタリマエ



5年算数 円と正多角形 2 わかる教え方のポイント




円周の公式 なぜ直径 円周率で計算できるのか 円周率を調べる方法 数学fun
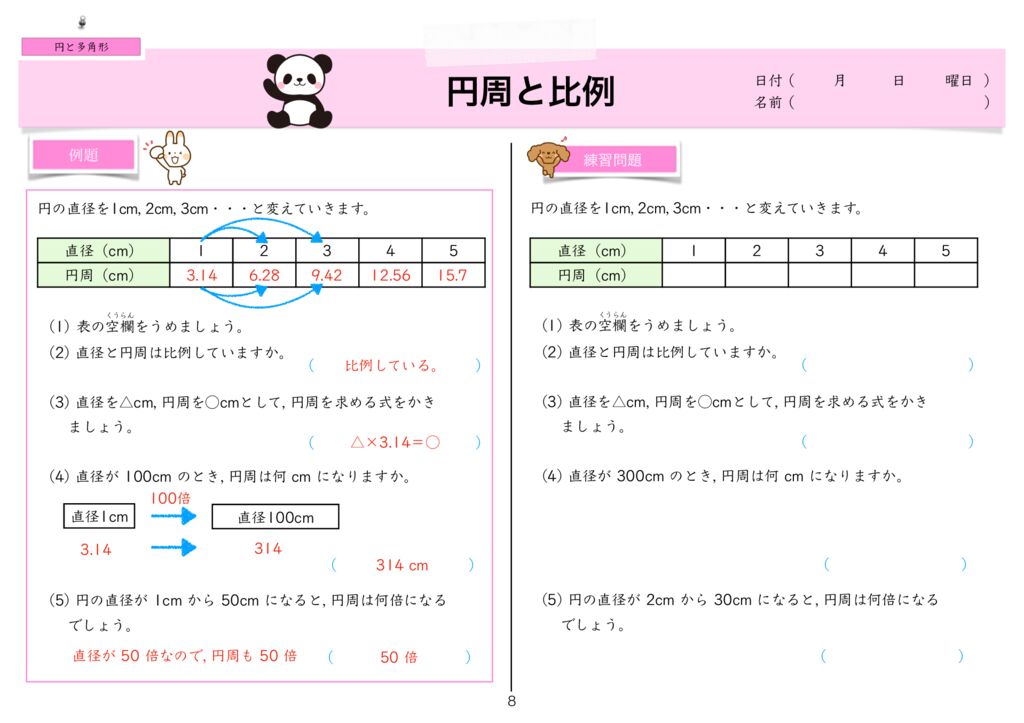



世界一分かりやすい算数 小5 円と正多角形




5年算数 円と正多角形 2 わかる教え方のポイント
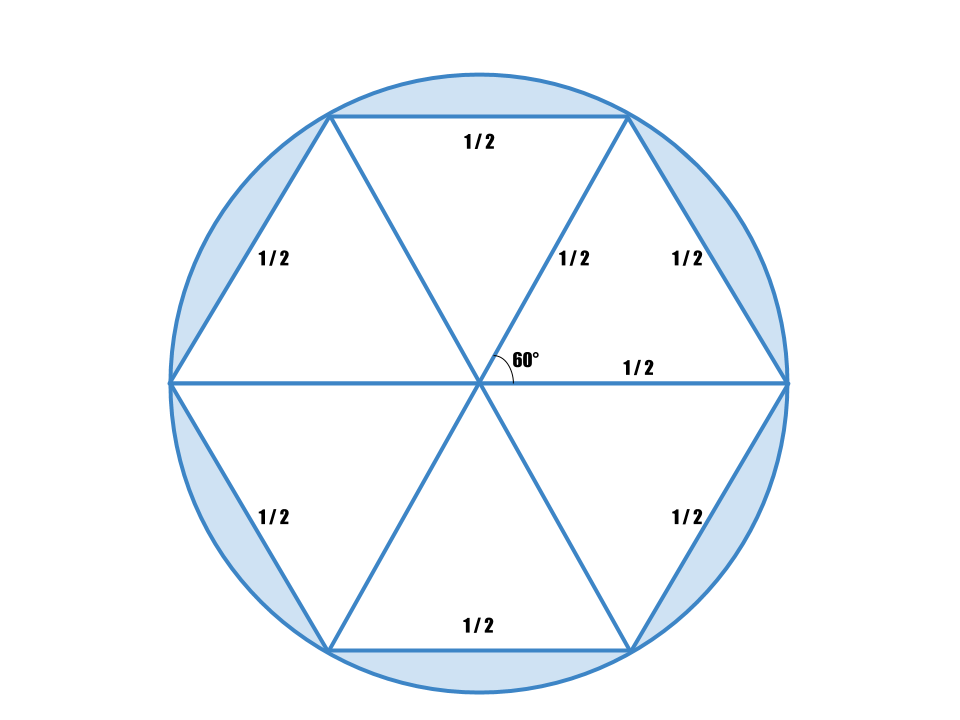



東大入試解説 円周率が3 05よりも大きいことを証明せよ



5年算数 円と正多角形 2 わかる教え方のポイント



3月14日は円周率の日 P 3 14 フロント講師が教える成績アップ術




小学5年生の算数 円 おうぎ形 問題プリント ちびむすドリル 小学生




円と正多角形 5年 算数 プロカリ



Www City Kita Tokyo Jp Gakkoshien Kosodate Shogakko Gakkojoho Kuritsu Takinogawa 02 Documents 5nen14 Seitakakukei En Test1 Pdf
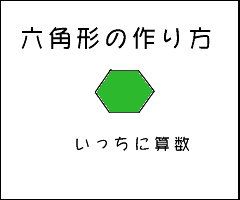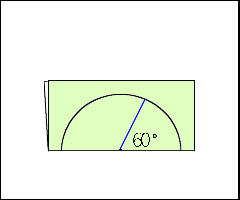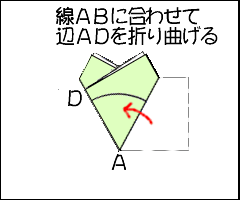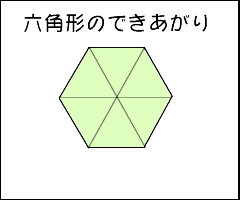



5年算数 円と正多角形 1 わかる教え方



5年算数 円と正多角形 1 わかる教え方



三平方の定理から円周率を計算してみる Yamav1 02bのブログ
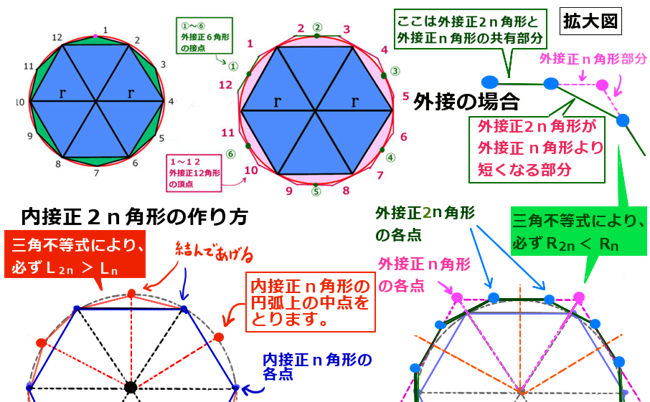



極限値としての円周率の存在証明 理数系無料オンライン学習 Kori




正多角形を定規だけで描く 交点座標から線で結ぶ方法 Alumania Information
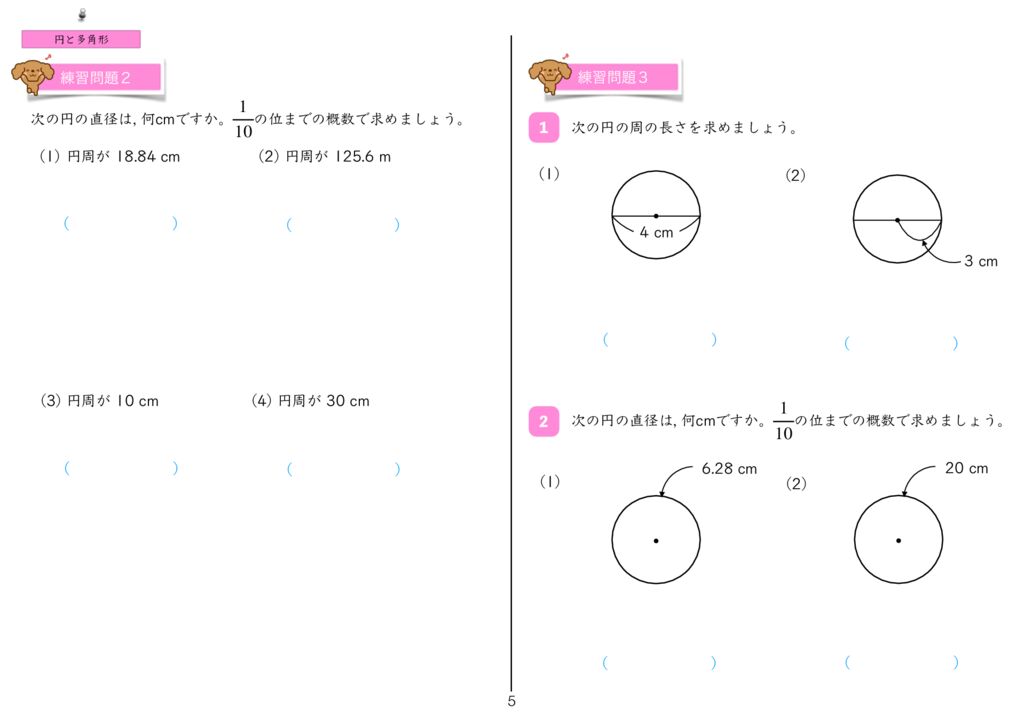



世界一分かりやすい算数 小5 円と正多角形




円の面積基本b 学習ノート 学習 数学教室



正多角形と円周の長さ 円周の公式 そばに書く癖 小学5年 算数の教え方教えますmother S Math Happy Study Support



Http Www City Akishima Ed Jp Nakagami 5nen Sansuu Pdf
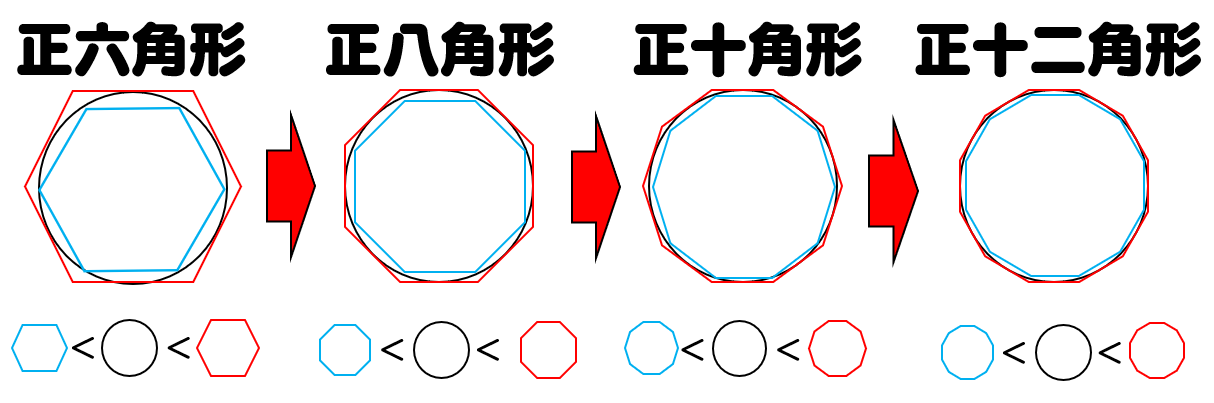



円周の公式 なぜ直径 円周率で計算できるのか 円周率を調べる方法 数学fun
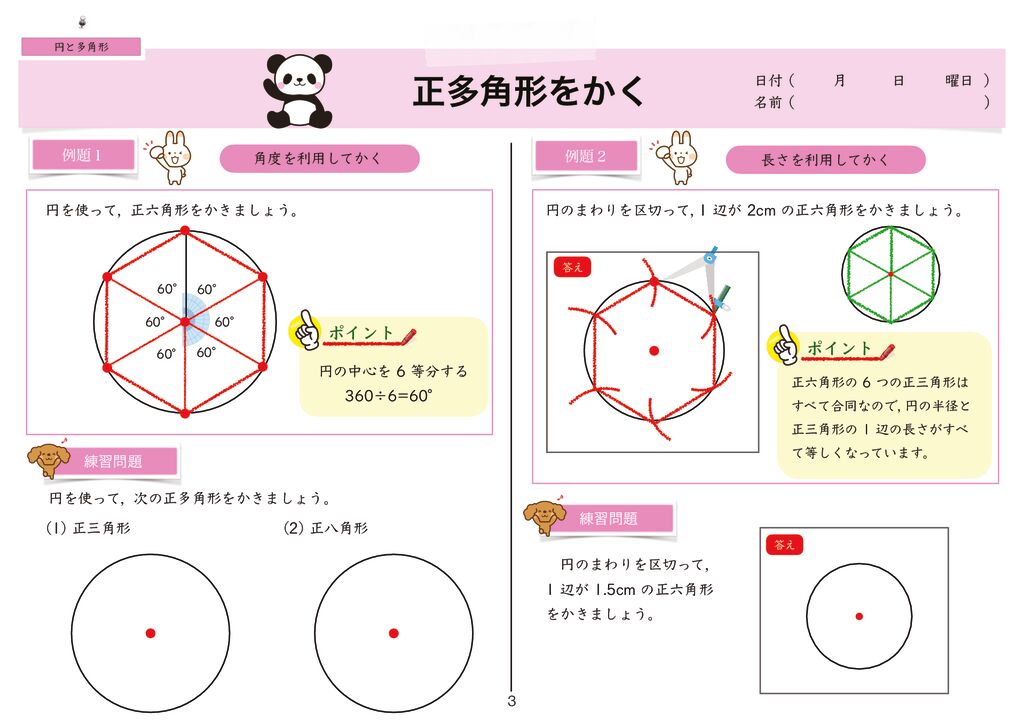



世界一分かりやすい算数 小5 円と正多角形



5年算数 円と正多角形 2 わかる教え方のポイント
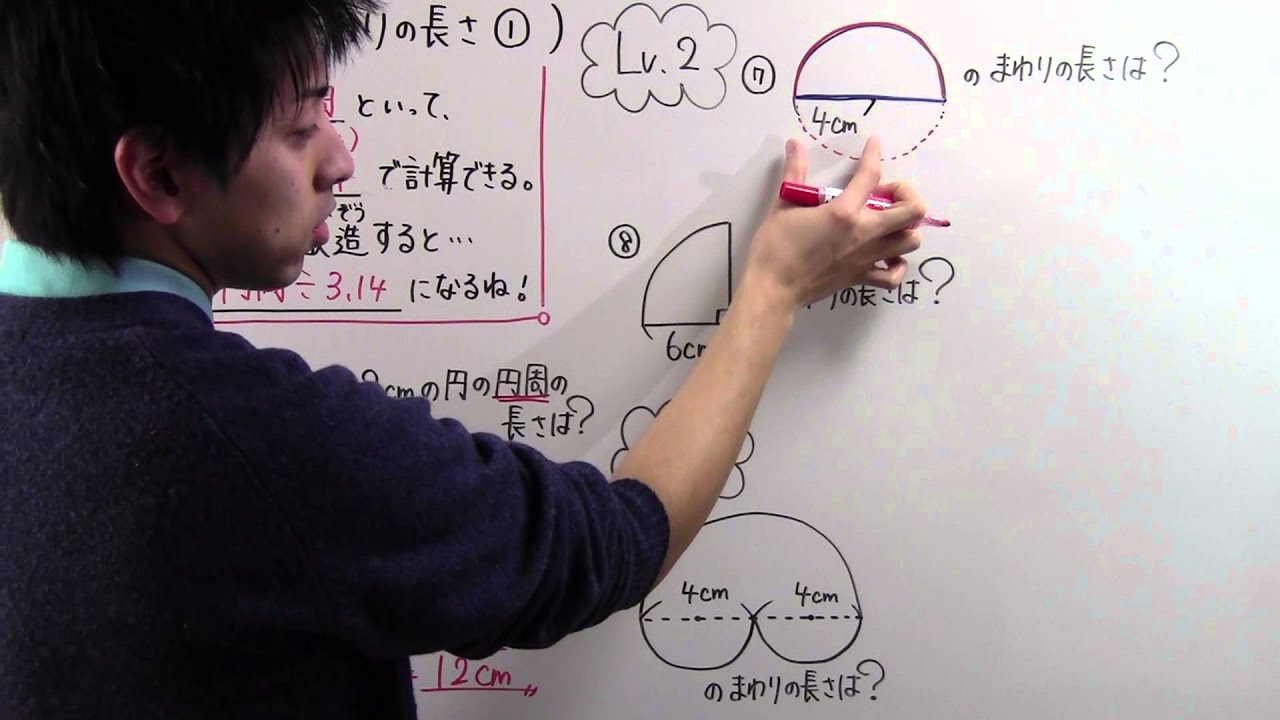



小5 算数 小5 55 円のまわりの長さ Youtube




すきるまドリル 小学5年生 算数 多角形と円 無料学習プリント すきるまドリル 無料学習プリント




正多角形を定規だけで描く 交点座標から線で結ぶ方法 Alumania Information




図形 奇数の正多角形の直径算出 奇数の正多角形 三角 五角 七角 数学 教えて Goo



円周率 P とは 求め方や100桁までの覚え方をご紹介 受験辞典
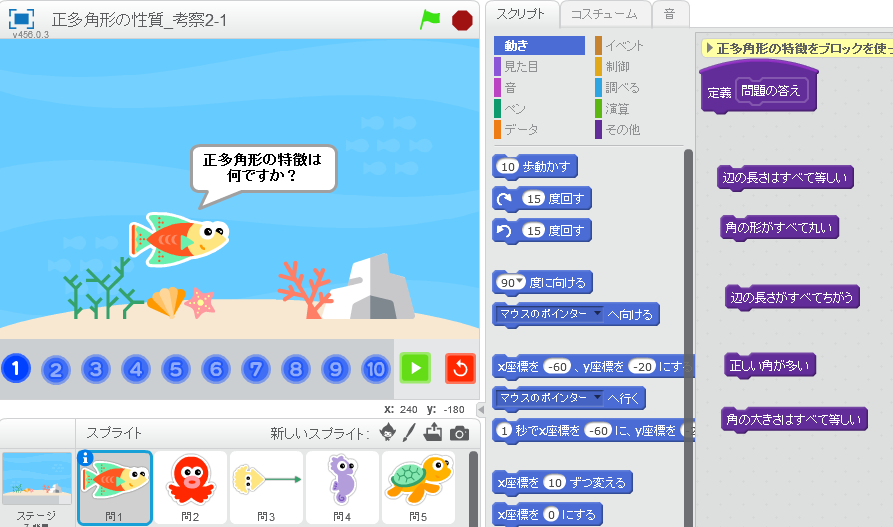



正多角形と円周の長さ プロアンズ



5年算数 円と正多角形 2 わかる教え方のポイント




正多角形をプログラムを使ってかこう 杉並区立西田小学校 未来の学びコンソーシアム
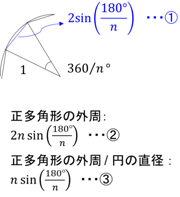



計算コラム 高精度計算サイト



1



Q Tbn And9gcsg0xroggdbomj506figjv69kistmku5ydmyoemnqkvaux8s4nt Usqp Cau




小学5年生 円周率 円のまわりの長さ 算数 Active Learning 学院



正多角形と円周の長さ 応用問題2 面倒くさがらせないで 小学5年 算数の教え方教えますmother S Math Happy Study Support




小学5年生の算数 円 おうぎ形 問題プリント ちびむすドリル 小学生



世界一分かりやすい算数 小5 円と正多角形




メルカリ Usb付き フラッシュカード 小5 円と正多角形 文房具 1 999 中古や未使用のフリマ




円周率 算数用語集



そういやp 円周率 ってどうして正確に求められないのか という謎 Edtech Inno



Http Www2 Synapse Ne Jp Tanaka Es Pdf Sidouan 5nen Sansu Pdf



すきるまドリル 小学5年生 算数 多角形と円 無料学習プリント すきるまドリル 無料学習プリント




正多角形を定規だけで描く 交点座標から線で結ぶ方法 Alumania Information
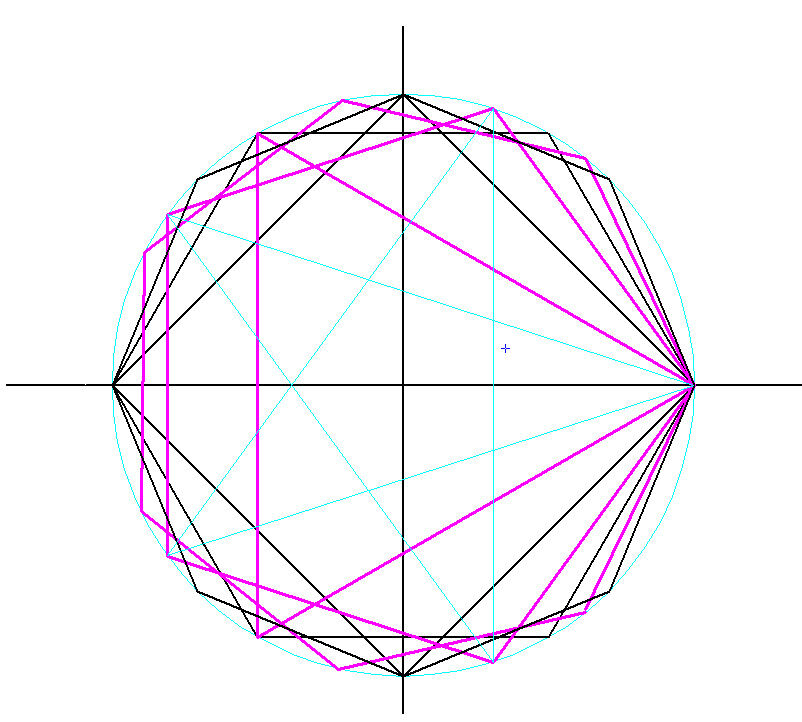



正多角形の角数 偶数奇数 と人類の至宝e Ip ー1の幾何学的関係 発想力教育研究所 素数誕生のメカニズム



Http Www Nc Gunma Boe Gsn Ed Jp Action Common Download Main Upload Id 2719
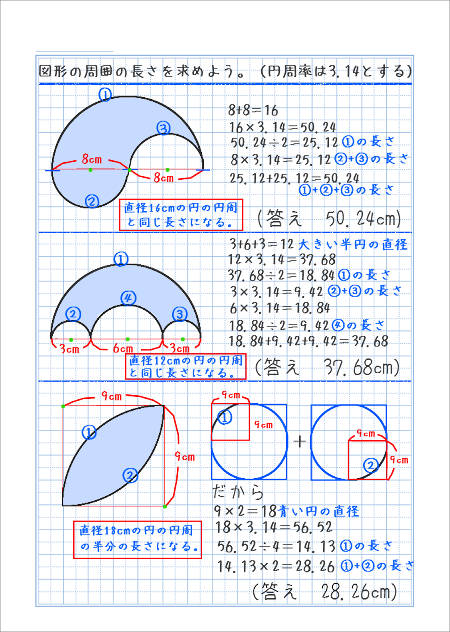



円周の長さの問題をもっと解いてみよう 家庭学習レシピ



エッセイ68 パパの夏休みの宿題 円周率p パイ
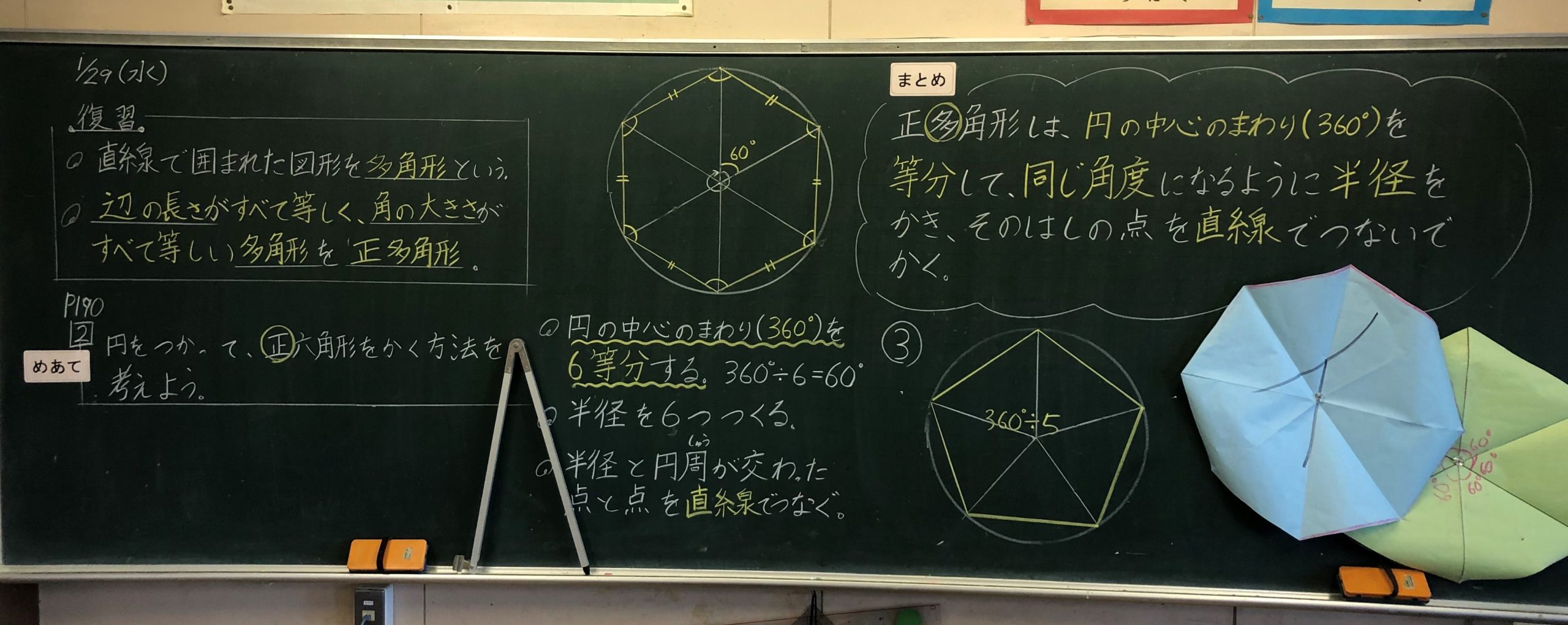



5年生算数 円と正多角形 黒板log
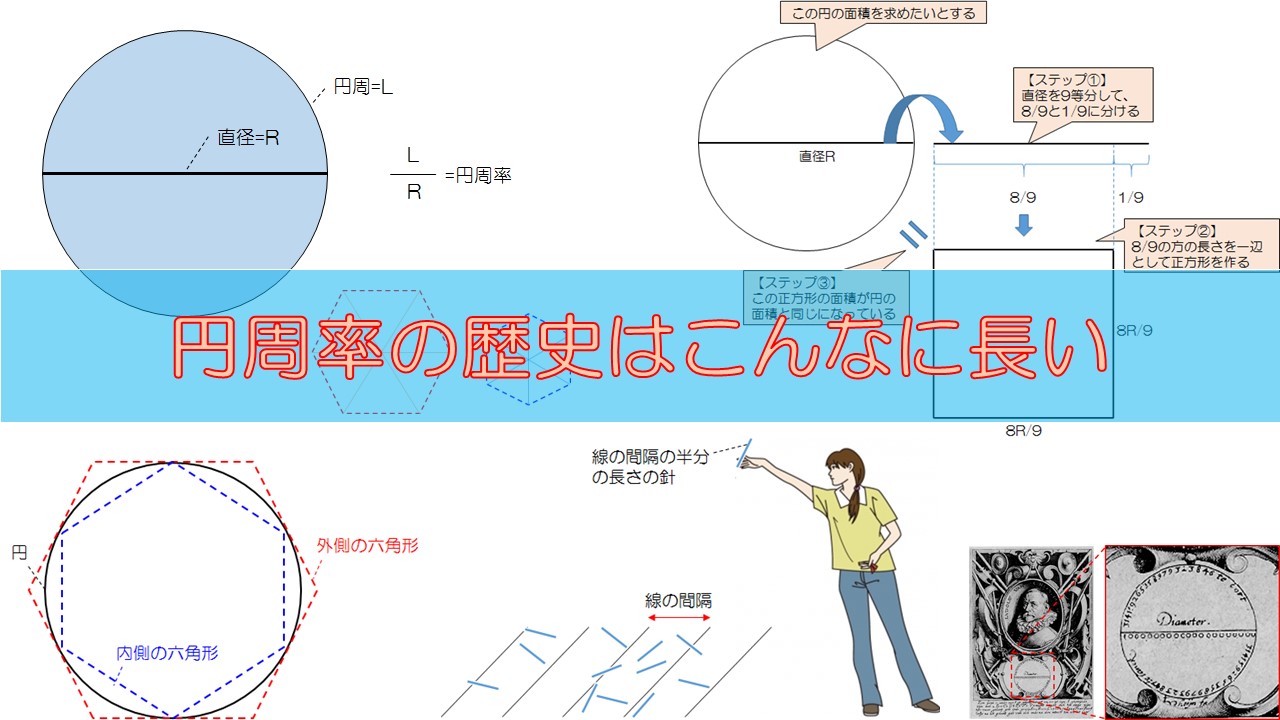



面白い円周率の歴史 昔の人たちはこうやって3 14 を求めてた 数学の面白いこと 役に立つことをまとめたサイト




小学5年生 円周率 円のまわりの長さ 算数 Active Learning 学院




円の面積3 小学校6年生の教科書から つづき 身勝手な主張



少人数教室から



5年算数 円と正多角形 2 わかる教え方のポイント



Http Www Edu Tens Net Kyouikuken Basic Takamatsu Pdf Esan5 Answer S5 11ans Pdf
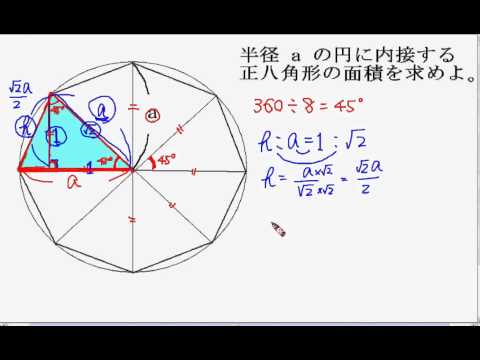



中3数学 正八角形の面積 Youtube



Http Www Kita9 Ed Jp Eductr Handbook Challengesheet Elementaryschool Sansuu 5 513 Pdf




世界一分かりやすい算数 小5 円と正多角形




高校数学a 正多角形内の三角形の個数 二等辺三角形 正三角形 直角三角形 鈍角三角形 鋭角三角形他 受験の月



1
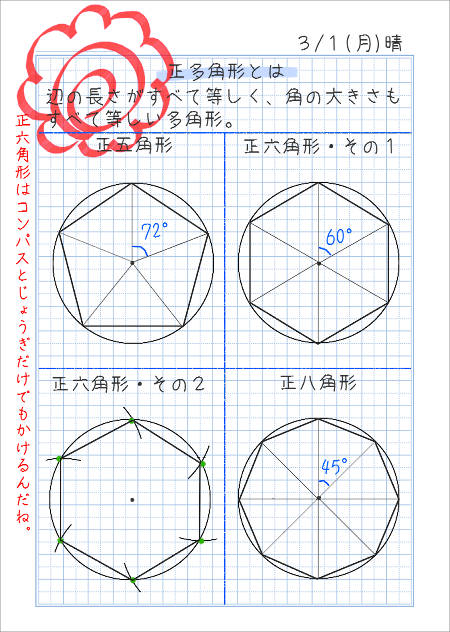



いろいろな正多角形をかいてみよう 家庭学習レシピ




円の周りの長さを計算しよう 家庭学習レシピ
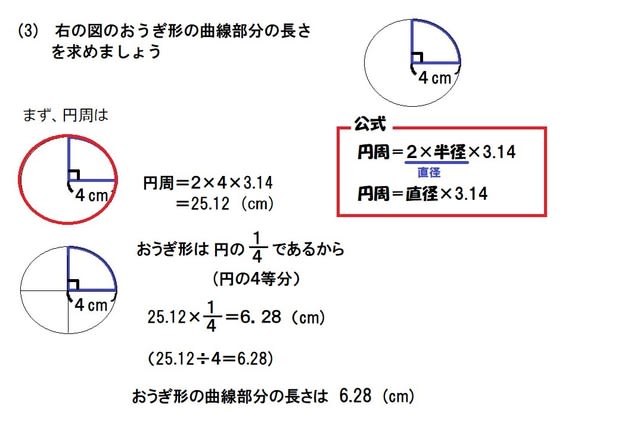



正多角形と円周の長さ 円周の公式 そばに書く癖 小学5年 算数の教え方教えますmother S Math Happy Study Support
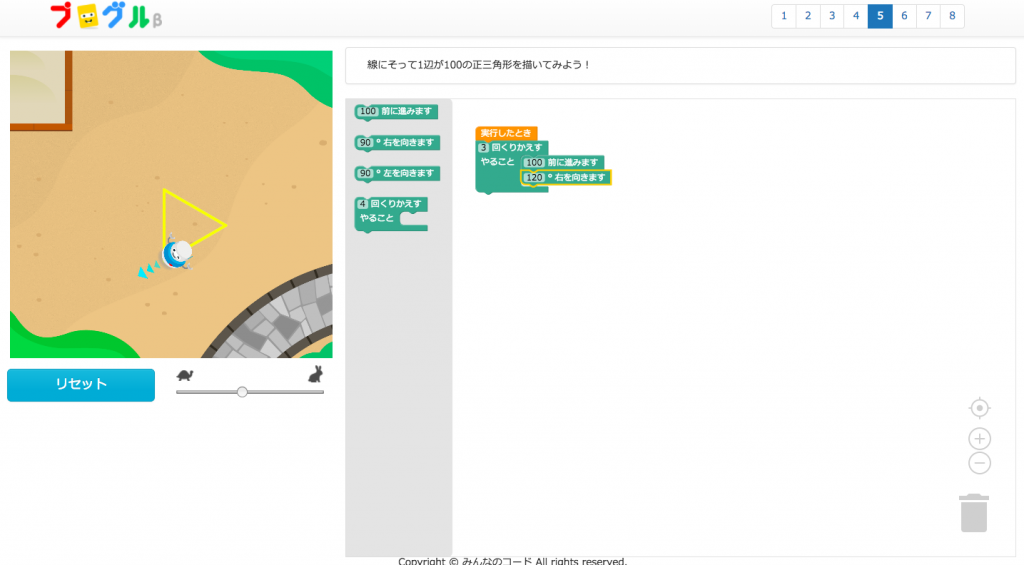



プログラミング教育 算数の指導案 正多角形 プログラミングで 平面図形の理解を深め 算数の深い学びにつなげる




正多角形と円周の長さ 円周の公式 そばに書く癖 小学5年 算数の教え方教えますmother S Math Happy Study Support



円周率 P とは 求め方や100桁までの覚え方をご紹介 受験辞典



コンパスと定規を使った正六角形の描き方 図形の描き方012a 夏貸文庫
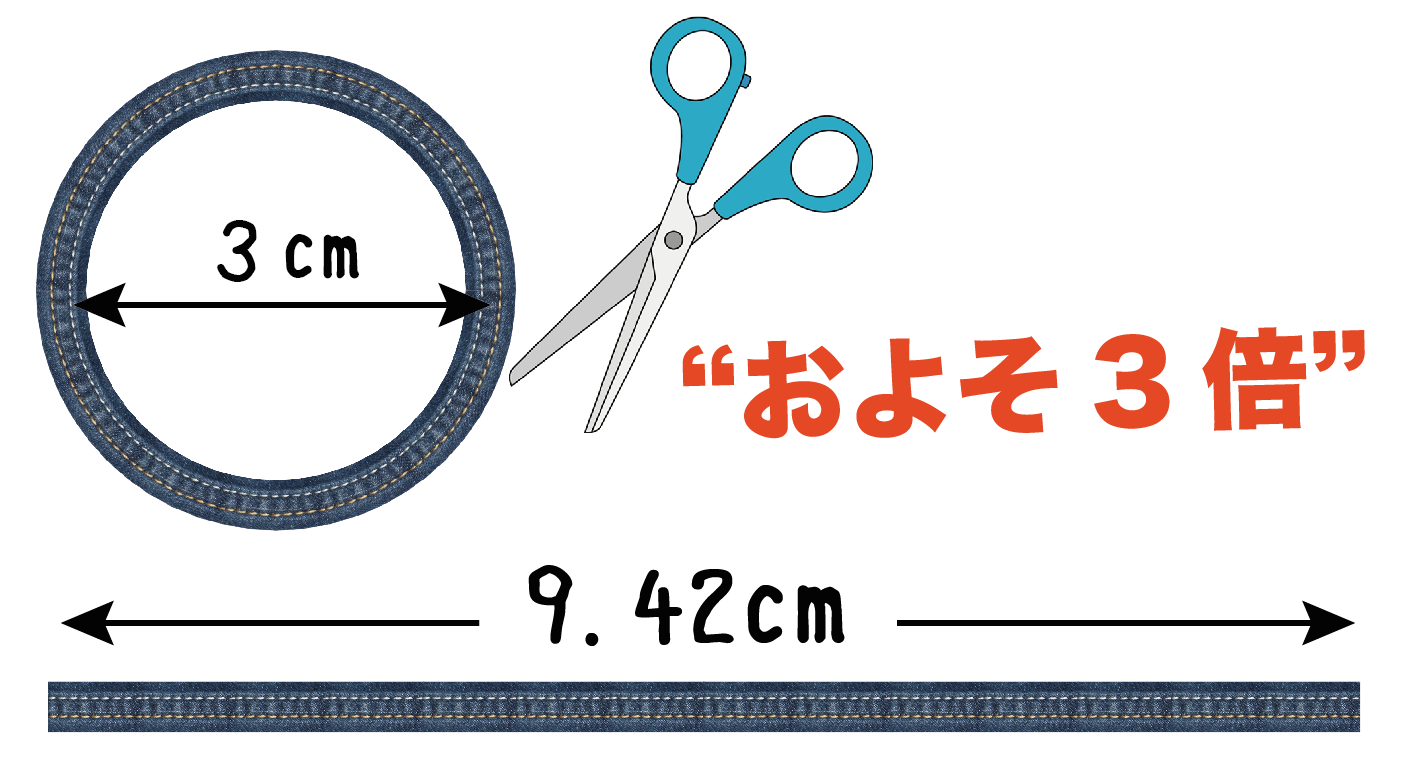



直径から計算 円周の長さの求め方 の公式を3秒で覚える方法 Qikeru 学びを楽しくわかりやすく
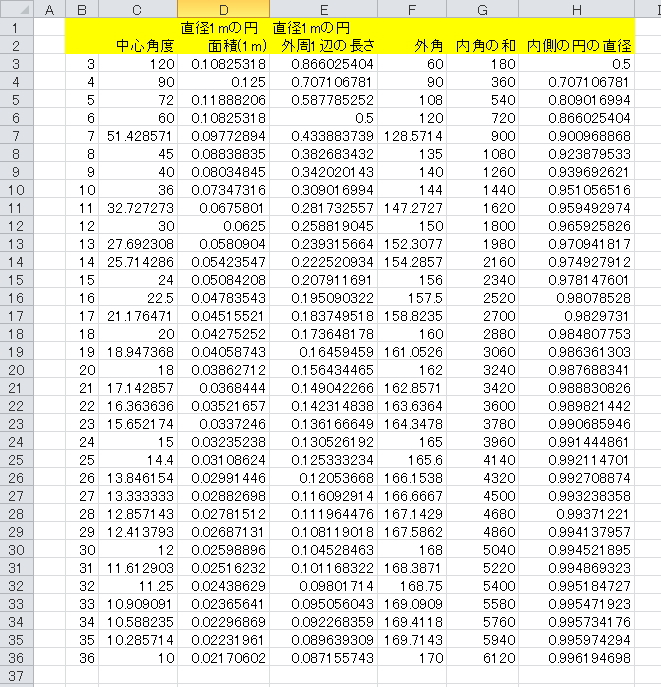



正 角形 正多角形 を表にしてみる エクセル関数の使い方




5年算数 円と正多角形 1 わかる教え方
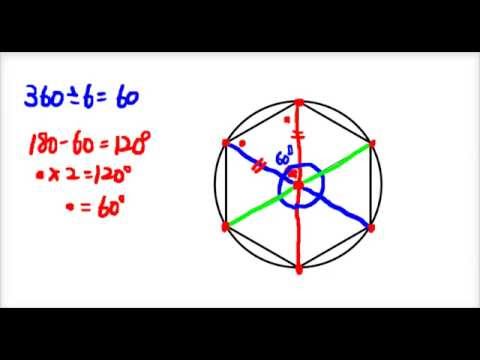



簡単にわかる 正六角形のかきかた ふるやまんの算数塾 Youtube




小5算 円の周りの長さ1 説明1 円周と直径の関係 円周率が3より大きく4より小さい理由 Youtube



円周率 算数用語集
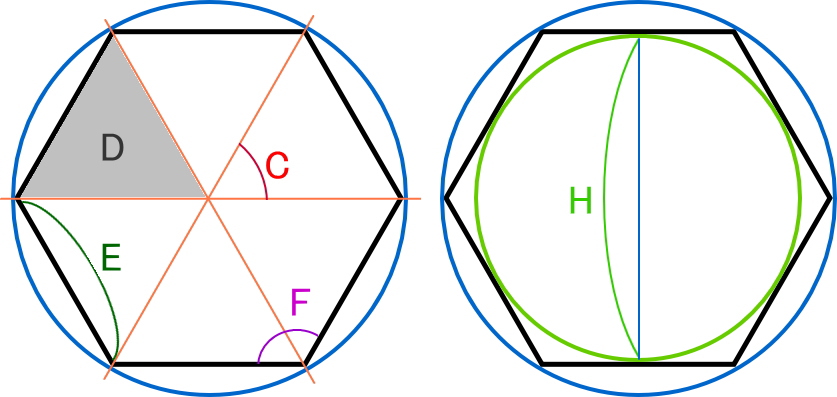



正 角形 正多角形 を表にしてみる エクセル関数の使い方




機械設計のための基礎製図



Www City Adachi Tokyo Jp Documents Em 5 15 Pdf
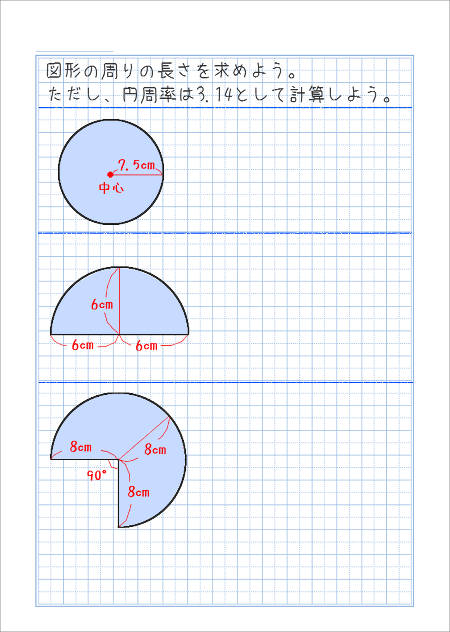



円の周りの長さを計算しよう 家庭学習レシピ




機械設計のための基礎製図



5年算数 円と正多角形 2 わかる教え方のポイント




正多角形と円周の長さ 円周の公式 そばに書く癖 小学5年 算数の教え方教えますmother S Math Happy Study Support




5年生算数 円と正多角形 黒板log
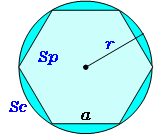



正多角形の外接円 高精度計算サイト




メルカリ Usb付き フラッシュカード 小5 円と正多角形 文房具 1 999 中古や未使用のフリマ
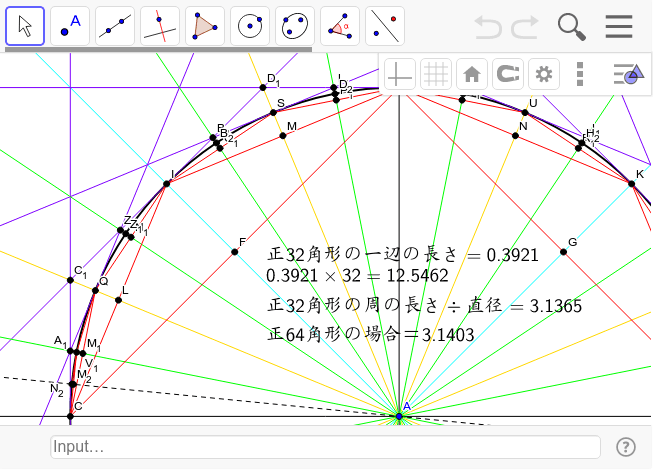



円周率の計算 Geogebra
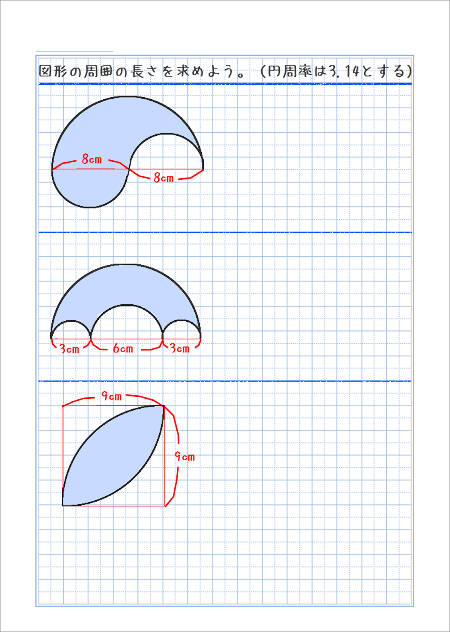



円周の長さの問題をもっと解いてみよう 家庭学習レシピ
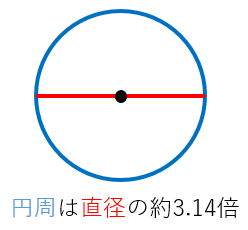



円周の長さの求め方と例題 具体例で学ぶ数学
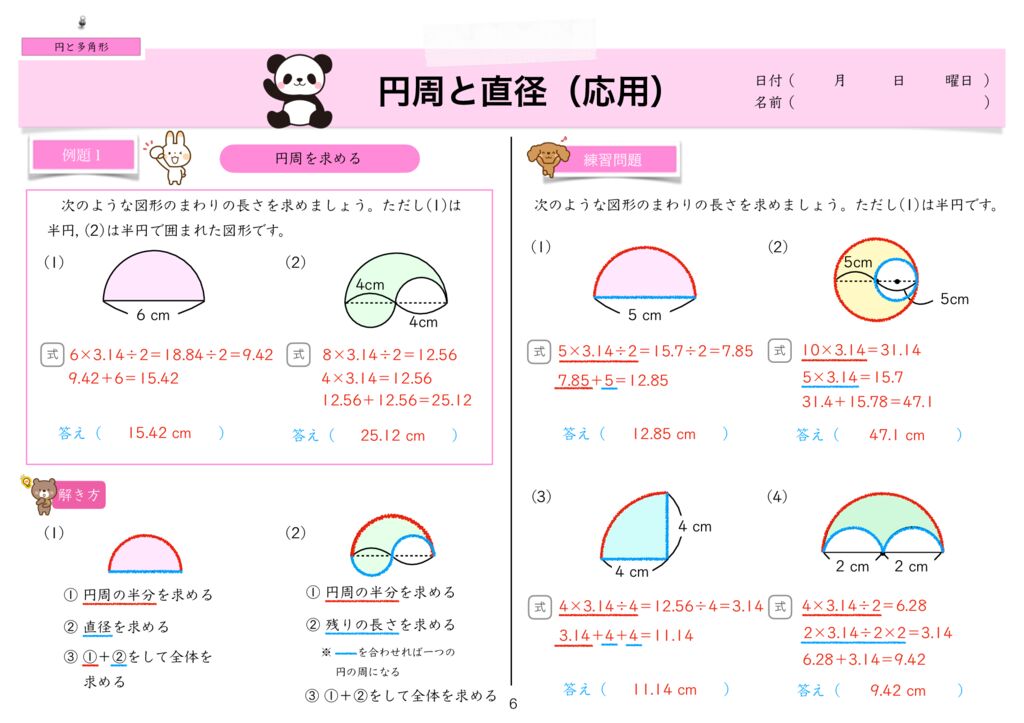



世界一分かりやすい算数 小5 円と正多角形
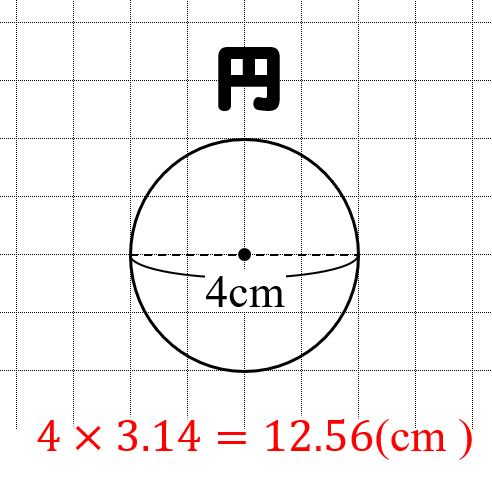



円周の公式 なぜ直径 円周率で計算できるのか 円周率を調べる方法 数学fun




円周の公式 なぜ直径 円周率で計算できるのか 円周率を調べる方法 数学fun
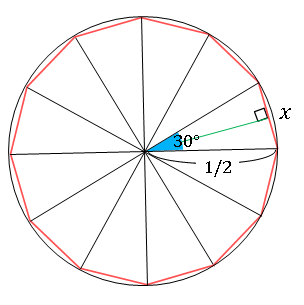



円の面積と周長



0 件のコメント:
コメントを投稿